Cytowane w poprzednim artykule przeogromne liczby związane z potencjalną liczbą kopiowań łańcuchów nukleotydowych będących nośnikami projektów obiektów żywych dają wiele do myślenia.
Dziś chciałbym poruszyć właśnie temat myślenia. Po raz pierwszy z faktem, że jest coś „co nie mieści się w głowie” spotkałem się w wieku chyba 10 lat. Czytałem wówczas książkę o szachach i natrafiłem na opowieść o ziarnach.
„Według wielu źródeł szachy powstały w VI wieku przed naszą erą w Indiach. Z ich powstaniem wiąże się ciekawa legenda.
Mędrzec Sissa Nassir, który wynalazł szachy tak zachwycił grą swojego władcę, że ten, aby wynagrodzić swojego poddanego obiecał mu nagrodę. Mędrzec sam miał wybrać, czego od króla oczekuje. Ten nie namyślając się długo poprosił o liczbę ziaren pszenicy, którą wyznaczy szachownica w następujący sposób:
Połóż panie na pierwszym polu szachownicy jedno ziarno, na drugim dwa, na kolejnych cztery, osiem, szesnaście i tak do ostatniego pola za każdym razem podwajając ich liczbę.
Władca był zdumiony skromnością prośby swojego poddanego, jednak szybko okazało się, że w całych Indiach nie ma takiej ilości zboża, by spełnić życzenie mędrca.
Historię tą można usłyszeć w różnych wersjach, raz rzecz dzieje się w Indiach, kiedy indziej w Persji, bohaterem jest mędrzec lub ubogi chłop… Jest stara jak same szachy i zapewne zmyślona, obrazuje jednak jaka drzemie w nich matematyczna moc.
Życzenie mędrca rzeczywiście jest niemożliwe do spełnienia.
Zobaczmy, jak można zapisać ilość ziaren na szachownicy:
1 pole 1=20, 2 pole 2=21, 3 pole 4=22, 4 pole 8=23 i tak aż do ostatniego 64 pola, na którym znajdzie się 263 ziaren.
Ilość wszystkich ziaren jest sumą pewnego ciągu geometrycznego i daje nieprawdopodobnie wielką liczbę 18 446 744 073 709 551 615, czyli ponad 18 trylionów! Aby zgromadzić taką ilość pszenicy królewski spichlerz o wysokości 4 i szerokości 10 metrów, musiałby mieć długość aż 300 milionów kilometrów, a gdybyśmy chcieli kłaść na szachownicy jedno ziarno na sekundę, zajęłoby nam to 585 miliardów lat, czyli o wiele więcej niż wynosi wiek Wszechświata!” [Źródło: http://blog2pir.blogspot.com/2014/02/ziarna-pszenicy-na-szachownicy.html]
Zaiste, nie mieści się to w głowie, żeby ta na pozór błaha prośba okazała się niemożliwa do spełnienia. Po prostu „nie czujemy” wzrostu wykładniczego. Jest on dla nas nieintuicyjny.
Po raz drugi, z czymś co nie pasowało do moich przekonań spotkałem się samym początku studiów. Już na pierwszym wykładzie z mechaniki klasycznej oznajmiono nam, że „do tej pory mechaniki byliśmy uczeni w niewłaściwy sposób” i w związku z tym teraz najważniejszym zadaniem naszych wykładowców będzie oduczenie nas wyuczonych w szkole średniej schematów myślenia. Z grubsza chodziło o to, że w szkole dla danych zagadnień podawano nam gotowe wzory na przysłowiową wiarę, po czym my podstawialiśmy do nich konkretne wartości liczbowe by rozwiązać zadanie. Na studiach mieliśmy się nauczyć analizować badane zjawisko po to by w postaci układu równań różniczkowych i całkowych zbudować jego model, z niego wyprowadzić wzory i dopiero do nich podstawiać wartości liczbowe.
Po raz trzeci mój naukowy światopogląd został poddany weryfikacji, gdy zacząłem pracować w Instytucie Sportu. Jako inżynier byłem świecie przekonany, że wszystko da się zmierzyć, obliczyć i skonstruować – tylko „sky is the limit” (możliwości są praktycznie nieograniczone). Tym co odróżnia Instytut Sportu od innych placówek naukowych jest, zasadniczo inaczej sformułowany, cel naukowy – co należy zrobić by mój zawodnik zdobył złoty medal na Igrzyskach Olimpijskich? Nie ma na to wzorów! Tego nie da się obliczyć!
Wielkim dla mnie odkryciem okazała się dla mnie teoria gier. Praktycznie mało kto o niej wie, bo zupełnie nie wspomina się o niej w szkołach średnich. Natomiast, jeśli chodzi o wyższe uczelnie to jest wykładana zaledwie na kilku kierunkach. Z tego też względu matematyczna teoria gier jako narzędzie analizy rzeczywistości jest dla zdecydowanej większości z nas wysoce nieintuicyjne. Czują ją trenerzy i niektórzy wojskowi, ale dlatego, że nie używają formalizmu matematycznego to ani oni, ani my nie czujemy, że mają do czynienia z nauką.
John Maynard Smith (1920-2004) wprowadził elementy teorii gier do badań nad zachowaniami obiektów żywych, o czym wspomniał w książce „Samolubny gen” Richard Dawkins (1941-). Temat nieco szerzej opisał w książce „Nonzero. Logika ludzkiego przeznaczenia” dziennikarz Robert Wright (1957-) i w zasadzie na tym się skończyło. Nigdzie nie spotkałem się z twierdzeniem, że teoria gier jest jedną z najważniejszych dyscyplin naukowych niezbędnych do poznania procesów życiowych. Podkreślam – niezbędnych.
Jak to w matematyce, twierdzenie trzeba udowodnić – spróbujmy zatem.
Teoria gier to dział matematyki zajmujący się badaniem optymalnego zachowania w przypadku konfliktu interesów [Wikipedia pol., stan 2019.12.11]. Z kolei konflikt interesów to zjawisko spowodowane współzawodnictwem o ograniczone zasoby [Wikipedia pol., stan 2019.12.11].
Każdy obiekt żywy potrzebuje zasobów do zbudowania samego siebie i wydania potomstwa – jest to absolutnie niepodważalny fakt. Masa przeciętnej bakterii szacowana jest na około 1 *10-12 grama, a masa Ziemi na 6*1027 grama. Z obliczeń wynika, że wystarczają 133 podziały, by z jednej bakterii powstała kolonia jej potomków przekraczająca masę Ziemi! Oczywiście nie jest to możliwe, bo na Ziemi nie ma aż tylu wolnych zasobów. 133 podziały, a bakteria w sprzyjających warunkach dzieli się co 20 minut. 133 razy 20 minut daje 2660 minut, a 2660 minut to nieco ponad 44 godziny. Zatem w 44 godziny bakterie zużyłyby wszystkie zasoby objętości Ziemi do zbudowania samych siebie. „Gdyby oczywiście były sprzyjające warunki” – może ktoś zauważyć. Jasne, a jak w takim razie należy rozumieć przeciwieństwo „sprzyjających warunków”? No cóż, odpowiedź jest prosta – brak potrzebnych zasobów.
Jak zatem widać namnażające się obiekty żywe bardzo szybko doprowadzają do braku zasobów, do sytuacji, gdy pożądają ograniczonych zasobów, mówiąc jeszcze inaczej, do sytuacji, gdy muszą współzawodniczyć o ograniczone zasoby, czyli do sytuacji konfliktu interesów. A jak już wiemy konfliktem interesów zajmuje się matematyczna teoria gier. Czy ten dowód wymaga jeszcze jakichś wyjaśnień?
Drugą najważniejszą dyscypliną naukową niezbędną do zrozumienia życia jest… ekonomia. Według angielskiej Wikipedii ekonomia to nauka zajmująca się produkcją, przepływami (distribution) i zużywaniem (consumption) zasobów (goods and services) [Wikipedia eng., Stan 2019.12.11]. Tak jak pisałem nie da się zaprzeczyć, że obiekty żywe produkują wymieniają i zużywają zasoby, w żadnym jednak podręczniku do biologii, w żadnej monografii nie znalazłem informacji, że by wiedzieć o co chodzi w życiu trzeba posługiwać się nauką o zasobach.
Tak więc, by zrozumieć życie trzeba zmienić podejście do jego analizowania, trzeba wyskoczyć z gorsetu tego co wiemy, ze stereotypów wiedzy do tej pory nabytej i otworzyć się na nowe dyscypliny naukowe. I próbować wykorzystać je do analizy życia.
Gdyby ktoś zadał mi pytanie jakie są najważniejsze dyscypliny naukowe niezbędne do zrozumienia życia i jego powstania, wymieniłbym: teorię gier, ekonomię i… teorię stabilności – dyscyplinę jeszcze mniej znaną niż teoria gier.
Opowiem o niej w jednym z kolejnych artykułów.






Kurczę, a biologia i fizyka nie są konieczne do zrozumienia życia? Rozumiem, że matematyka to królowa nauka, ale chemia także by się nam przydała. A co z psychologią, socjologią? Jasne, na poziomie komórkowym są zbędne, ale abyśmy życie pojęli w pełni, to chyba potrzeba nieco więcej dyscyplin naukowych 🙂
Święta racja,
potrzebna jest cała paleta nauk. Natomiast ja próbowałem pokazać jakie są najważniejsze, oczywiście według mnie. Zresztą nawet do słowa „najważniejsze” można się przyczepić i to całkiem słusznie.
To może sformułuje to tak: ekonomia i teoria gier są kluczowe w zrozumieniu procesów życiowych, bez ich znajomości nie da się zrozumieć wielu rzeczy.
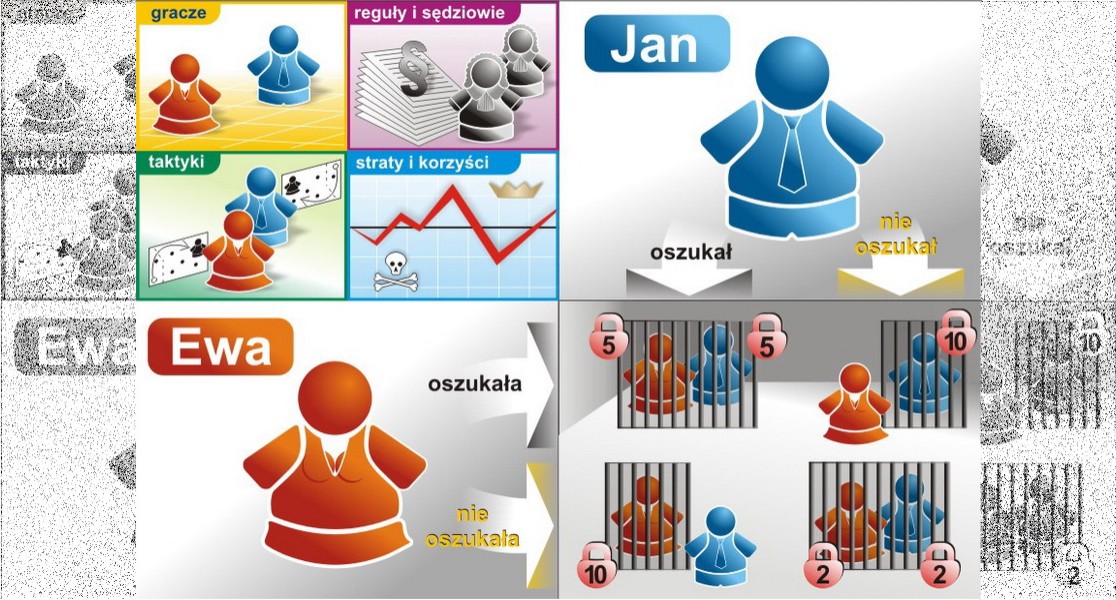
Ewa i Jan z obrazka tytułowego – uczciwość popłaca, ale w życiu mamy demonstrację cwaniactwa.
Ewa i Jan:
1. Oboje oszukują i odsiadują po 5 lat – razem 10 lat
2. Ewa oszukała – Jan odsiedzi sam 10 lat
3. Jan oszukał – Ewa odsiedzi 10 lat
4. Oboje są uczciwi i otrzymują po 2 lata – razem 4 lata.
Cenna uwaga. W tym przykładzie zastosowano taką a nie inną tabelę wypłat (w moim odczuciu dość życiową, czyli taką z jaką mamy w życiu do czynienia).
Pokazuje ona, że jeśli obie strony są uczciwe to populacja na tym zyskuje. Jednak jeśli jedna strona przycwani (czyli oszuka, gdy druga będzie uczciwa) to zyska bardzo dużo kosztem tej drugiej, uczciwej strony. Natomiast jeśli obie strony oszukują to populacja na tym traci.
Dylemat aresztowanych (mylnie nazywany dylematem więźnia) pokazuje dylemat celów indywidualnych versus społecznych. Takich modeli jest więcej i stopniowo będziemy je omawiać.
W życiu jednak jednostki chcą dominować nad innymi i całymi populacjami. Ludzie niby są istotami społecznymi, ale ich aspiracje są ponadspołeczne. Mając ewidentne przykłady, że dominacja popłaca – jest się ponad prawem, ponad wszystkimi, ludzie łamią reguły i nie biorą pod uwagę dobra wspólnego, tylko indywidualne. Po nas choćby Potop.
Dlatego tak jaskrawo odbija się to w polityce, gdzie tę bezkarność i łamanie prawa i wszelkich reguł widać.
Jak wobec tego Ewa czy Jan mieliby myśleć inaczej, niż w kategoriach innych, niż przedkładanie interesu własnego nad wspólny.
Dokładnie tak. Ale problem ten w dość dużym stopniu rozwiazali Szwajcarzy swoim unikalnym w skali światowej systemem politycznym. Świetnie wprowadza na czym on polega książka Joanny Lampki „Czy wiesz, dlaczego nie wiesz, kto jest prezydentem Szwajcarii?”
Szwajcaria to bardzo dziwny kraj. Nie ma narodu szwajcarskiego, to bowiem zbiorowisko różnych nacji, ale jako kraj i gospodarka radzą sobie świetnie. Niemniej ten unikalny system polityczny i tak nie zastąpi braku moralności i dążenia do dominacji.
Tak jak w Polsce – zrywy niepodległościowe, współpraca przeciw wspólnemu wrogowi, ale kiedy tego wroga nie ma, to partykularne interesy decydują.
To jest naprawdę zadziwiające, że ludzkość osiągnęła tak wiele i w ogóle jeszcze istnieje, przy takim podejściu do życia, które sprowadza się do ciągłej walki o dominację, zamiast do współpracy.
Z drugiej strony ciekawe gdzie byśmy byli już dziś, gdyby ludzkość miała tę współpracę we krwi.
Według mnie system polityczny kształtuje osobowość. Przeciętny Szwajcar zachowuje się inaczej niż przeciętny Polak. Ma też większe zrozumienie procesów społecznych i politycznych, i wreszcie jest bardziej samodzielny i bardziej odpowiedzialny. A to wszystko dlatego, że tak ich ukształtował system demokracji bezpośredniej.
„Jak wobec tego Ewa czy Jan mieliby myśleć inaczej, niż w kategoriach innych, niż przedkładanie interesu własnego nad wspólny?”.
Mogą być do tego zmuszeni, na przykład w tedy gdy od współpracy zależy ich życie, a brak współpracy skazuje ich na śmierć.
Polecam przestudiowanie Iterowanego Dylematu Aresztowanych, błędnie acz powszechnie zwanego Iterowanym Dylematem Więźnia.